Materi Program Linier

Kelas XII IPS

Pertidaksamaan Linier Dua Variabel

Pertidaksamaan ini secara umum ditulis dengan bentuk

ax + by ≤ c atau ax + by ≥ c

dalam materi program linier akan sering muncul kalimat matematika yang harus sobat terjemahkan ke dalam bentuk pertidaksamaan di atas. Selanjutnya sobat harus bisa menggambarkannya dalam bidang cartesius dan menentukan daerah hasilnya. Pertidaksamaan tersebut mempunyai penyelesaian berupa himpunan pasangan (x,y) yang memenuhi pertidaksamaan. Nah bentuk penyelesaiannya dapat digambarkan dalam koordinat bidang cartesius dan hasilnya merupakan daerah arsiran.

Contoh Soal

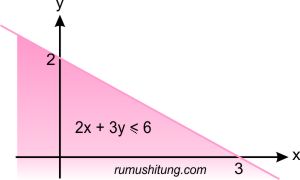
Tentukan penyelesaian dari pertidaksamaan 2x + 3y ≤ 6

Alternatif cara menjawabnya

• Langkah 1gambar garis 2x + 3y = 6 pada diaragm cartesius dengan terlebih dahulu meneetukan titik potongnya pada sumbu x maupaun ytitik potong sumbu x (y=0)
  2x + 3y = 6
  2x + 0 = 6
  x = 3 → (3,0) titik potong sumbu y (x = 0)
  2x + 3y = 6
  0 + 3y = 6
  y = 2 → (0,2) gambar gari tersebut tampakGambar persamaan garis
• Langkah 2Sobat hitung perhatikan tanda pertidaksamaan dan koefisien x untuk menentukan daerah arsiran. Cobalah memasukkan nilai x (misal saja 0) jika memenuhi persamaan maka sisi area dimana titik x = 0 berada merupakan daerah hasil.

Apa Itu Program Linier?

Yang dinamakan program linier adalah sebuah kumpulan aturan yang di dalamnya terdapat sebuah fungsi linier sebagai fungsi tujuan dan sebuah sistem pertidaksamaan linier yang berperan sebagai batas (fungsi pembatas). Program linier untuk dua variabel ditulis:

Fungsi yang menghasilkan nilai maksumum

f(x,y) = c₁x + c₂y

dengan batasan

a₁x + b₁y ≤ c
a₂x + b₂y ≤ c dengan x ≥ dan y ≥ 0

Sekarang yang menjadi pertanyaan adalah, “Bagaimana menemukan titik x dan y yang menghasilkan nilai maksimum?” Check this ouuut…

Menentukan Nilai Maksimum Fungsi Tujuan dalam Program Linier

Untuk menentukan nilai maksimal dari soal program linier sobat dapat menggunakan cara dengan menggambarkan grafik dari pertidaksamaan yang ada. Berikut langkah-langkahnya :

1. Tentukan himpunan penyelesaian dari tiap pertidaksamaan lalu sobat gambarkan daerah hasilnya di diagram cartesius
2. Cari titik-titik ekstrim
3. Tentukan hasil atau nilai dari fungsi masing-masing titik ekstrim dan sobat akan menemukan nilai yang maksimum

Contoh :

Tentukan nilai maksimum dari fungsi f(x,y) = 3 x + 5 y dengan batasan

3x + y ≤ 6

x + 2y ≤ 4

x ≥ dan y ≥ 0

Jawab :

Kita gambarkan derah hasil dari pertidak samaan 3x + y ≤ 6 dan x + 2y ≤ 4 pada diagram cartesius

Pertidaksamaan	Titik Potong Sb x	Titik Potong Sb y
3x + y ≤ 6	(2,0)	(0,6)
x + 2y ≤ 4	(4,0)	(0,2

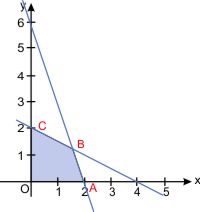
Dengan menggunakan yang telah kami jelaskan sebelumnya maka di dapat gambar :

Kita tentukan titik B yang merupakan titik potong dua pertidaksamaann menggunakan metode eliminasi (bisa juga substitusi)

3x + y = 6  [x 2] ⇒ 6x + 2y = 12
x + 2y = 4  [x 1] ⇒ x + 2y = 4
—————————————— –
——————– 5x = 8
——————–   x = 8/5
x + 2y = 4
16/5 + 2y = 4
2y = 4 – 8/5 = 20/5 – 8/5 = 12/5
y = 6/5

Dari diagram cartesius tersebut sobat dapatkan titik ekstrim

O (0,0) ; A (2,0) ; B (8/5,6/5) ; C (0,2)

Nilai f (x,y) = 3 x + 5 y kita cari untuk masing-masing titik ekstrim

f(O) = 0+0 = 0
f(A) = 3(2) + 5(0) = 6
f(B) = 3(8/5) + 5(6/5) = 54/5 = 10 4/5
f (C) = 3(0) + 5.2 = 10

Jadi nilai maksimal dari fungsi tujuan adalah 10 4/5  yang didapat pada kondisi (titik) B (8/5,6/5)

Menggunkan Garis Selidik

Ini sekedar tambahan buat sobat hitung. Dalam program linier nilai maksimum dari suatu fungsi tujuan sebenarnya dapat dicari dengan bantuan garis selidik. Bagaimana caranya? Sobat gambar dulu garis dari fungsi tujuan f(x,y). Kemudian geser garis tersebut pada titik-titik ekstrim pertidaksamaan pembatas. Amatilah di mana ketika posisi garis selidik dan daerah hasil dari pertidaksamaan menghasilkan daerah hasil yang paling banyak berada di bawah garis selidik. Itulah yang disebut titik maksimum.